In this post we present the essential parts of our method RINE, described in the paper Leveraging Representations from Intermediate Encoder-Blocks for Synthetic Image Detection, which has been accepted by the European Conference on Computer Vision (ECCV 2024).

Motivation

Recent research on Synthetic Image Detection (SID) has led to strong evidence on the advantages of representations extracted by foundation models, exhibiting exceptional generalization capabilities on GAN and Diffusion model generated data (Ojha et al. 2023). Motivated by this success, we hypothesize that further performance gains are possible by leveraging representations from intermediate layers, which carry low-level visual information, in addition to representations from the final layer that primarily carry high-level semantic information.

Method

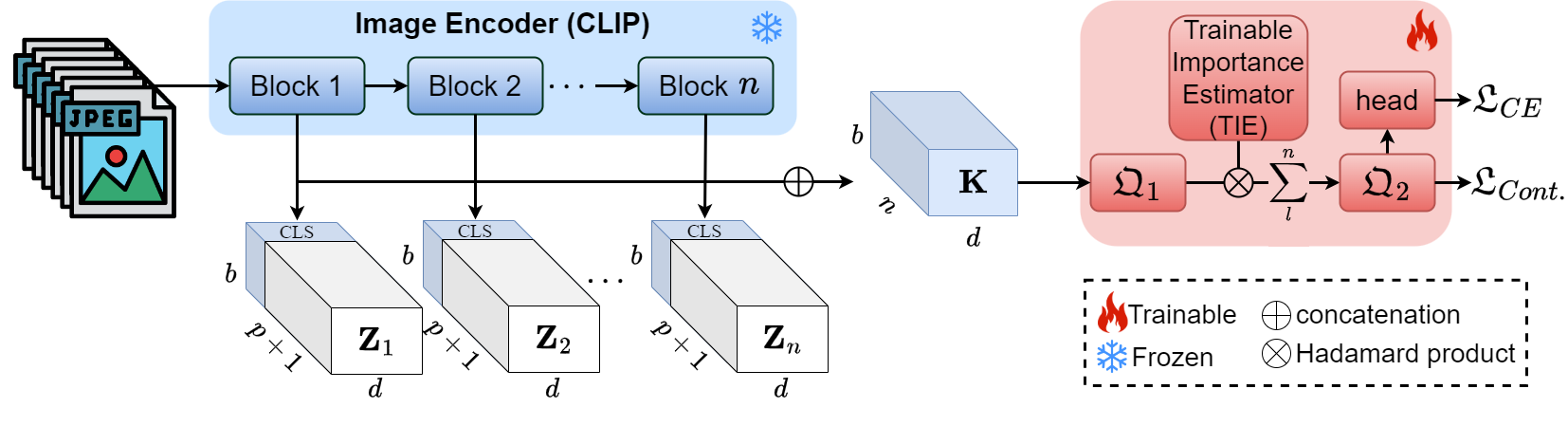
Feature Extraction

After the standard image pre-processing (patch extraction and projection, positional encoding), CLIP’s Visual Transformer processes the input tokens $\mathbf{Z}_0\in\mathbb{R}^{b\times (p+1)\times d}$ as below:

$$ \tilde{\mathbf{Z}_l}=\text{MSA}(\text{LN}(\mathbf{Z}_{l-1}))+\mathbf{Z}_{l-1} $$

$$ \mathbf{Z}_l=\text{MLP}(\text{LN}(\tilde{\mathbf{Z}_l}))+\tilde{\mathbf{Z}_l} $$

with $l$ denoting the block’s index.

Then, we define the Representations from Intermediate Encoder-blocks (RINE) $\mathbf{K}$, as the concatenation of CLS tokens from the corresponding $n$ blocks:

$$ \mathbf{K}=\oplus\lbrace\mathbf{Z}_l^{\text{[0]}}\rbrace_{l=1}^n\in\mathbb{R}^{b\times n\times d} $$

where $\oplus$ denotes concatenation, and $\mathbf{Z}_l^{\text{[0]}}\in\mathbb{R}^{b\times 1\times d}$ denotes the CLS token from the output of block $l$. We keep CLIP, which produces these features, frozen during training and use $\mathbf{K}$ to construct discriminative features for the SID task.

Learning

A projection network $\mathfrak{Q}_1$ with linear mappings, ReLU activations, and Dropout regulatizations, processes the input representations $\mathbf{K}$. Its output is then adjusted, with the use of a Trainable Importance Estimator (TIE) module, in order to reflect the importance of each Transformer block to the SID task:

$$ \tilde{\mathbf{K}}^{(ik)}=\sum_l^n\mathcal{S}(\mathbf{A})^{(lk)}\cdot\mathbf{K}_q^{(ilk)} $$

Another projection network $\mathfrak{Q}_2$ is then applied before the classification head that estimates the probability $\hat{y}_i$ of image $i$ to be fake.

Finally, we use a combination of binary cross-entropy and supervised contrastive loss to optimize our model:

$$ \mathfrak{L}_{CE}=-\sum_{i=1}^by_i\text{log}\hat{y}_i+(1-y_i)\cdot\text{log}(1-\hat{y}_i) $$

$$ \mathfrak{L}_{Cont.}=-\sum_{i=1}^b\frac{1}{G(i)}\sum_{g\in G(i)}\text{log}\frac{\text{exp}(\mathbf{z}_i\cdot \mathbf{z}_g/\tau)}{\sum_{a\in A(i)}\text{exp}(\mathbf{z}_i\cdot \mathbf{z}_a/\tau)} $$

$$ \mathfrak{L}=\mathfrak{L}_{CE}+\xi\cdot\mathfrak{L}_{Cont.} $$

Results

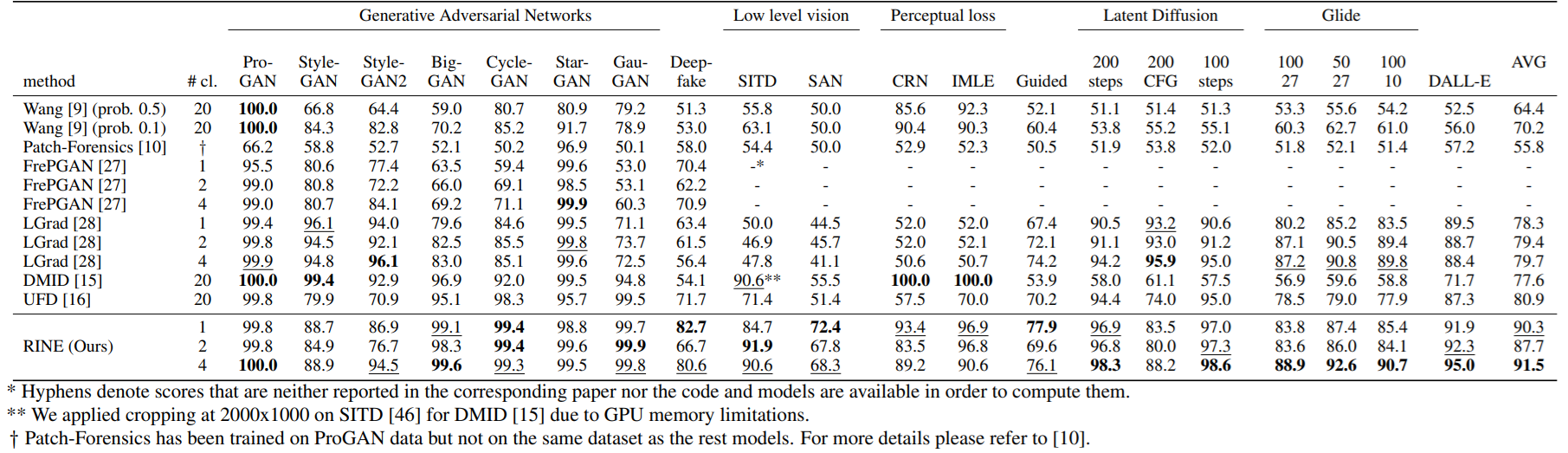
In the below Table, we present the performance of our method versus the competing ones in terms of accuracy. Our 1-class model outperforms all state-of-the-art methods irrespective of training class number. On average, we surpass the state-of-the-art by +9.4% with the 1-class model, by +6.8% with the 2-class model, and by +10.6% with the 4-class model. We obtain the best score in 14 out of 20 test datasets, and simultaneously the first and second best performance in 10 of them. The biggest performance gain is on the SAN dataset (+16.9%).

Additionally, in the paper you can find ablations that support our architectural choices, further experiments regarding robustness to perturbations, the effects of training duration, and training set size, the fact that considering more ProGAN object classes during training does not reduce generalization, and even more…

Code

Our code and model checkpoints are publicly available here https://github.com/mever-team/rine

References

Ojha, U., Li, Y., & Lee, Y. J. (2023). Towards universal fake image detectors that generalize across generative models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 24480-24489).

Wang, S. Y., Wang, O., Zhang, R., Owens, A., & Efros, A. A. (2020). CNN-generated images are surprisingly easy to spot… for now. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 8695-8704).